Chain Rule for Maps
$\newcommand\R{\mathbb{R}}\newcommand\C{\mathbb{C}}\newcommand\Z{\mathbb{Z}}$
Chain Rule for Map between Open Subsets of Euclidean Space
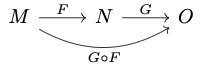
Let $M$ be an open subset of $\R^m$, $N$ be an open subset of $\R^n$, and $O$ be an open subset of $\R^p$. Let $$F: M \rightarrow N\text{ and }G: N \rightarrow O$$ be $C^1$ maps. We want to prove the chain rule for the composition:
Differential of a Map
Recall that the directional derivative of $F$ at $x \in M$ in the direction $v \in \R^m$ is defined to be $$ D_vF(x) = (F\circ c)'(0), $$ where $c: I \rightarrow M$ is a $C^1$ curve such that $$ c(0) = x\text{ and }c'(0) = v. $$ In other words, if $v \in \R^n$ is the velocity vector of a curve $c$ passing through $x \in M$, then $D_vF(x)$ is the velocity vector of the curve $F\circ c$ at $F(x)$.
It is easy to check that the map $$ v \mapsto D_vF(x) $$ is independent of the curve $c$ (as long as $c$(0)=x$ and $c'(0)=v$) and is linear. The differential of $F$ at $x$ is defined to be this linear map and is denoted $$ \partial F(x): \R^m \rightarrow \R^n. $$ This is also called the Jacobian and often written as a matrix of partial derivatives. We avoid doing that here.
Chain Rule
Given $x \in M$, we want to find the formula for the differential of $$ G\circ F: M \rightarrow O. $$
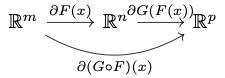
Given $x \in M$ and $v \in \R^m$, let $c: I \rightarrow M$ be a curve such that $c(0) = x$ and $c'(0) = v$. This in turn defines a curve $$ F\circ c: I \rightarrow N, $$ which satisfies $(F\circ c)(0) = F(x)$ and, repeating what we said above, \begin{align*} (F\circ c)'(0) &= \partial F(x)v. \end{align*} Therefore, \begin{align*} \partial(G\circ F)(x)v &= \left.\frac{d}{dt}\right|_{t=0}(G\circ F)(c(t))\\ &= \left.\frac{d}{dt}\right|_{t=0}G((F\circ c)(t))\\ &= \partial G(F(x))(F\circ c)'(0)\\ &= \partial G(F(x))\partial F(x)v\\ &= (\partial G(F(x))\circ\partial F(x))v \end{align*} This proves the chain rule $$ \partial(G\circ F)(x) = \partial G(F(x))\circ \partial F(x), $$
as depicted here:
Chain Rule for Maps Between Manifolds
Since everything above is done without using coordinates, the same proof works for manifolds.
Let $M$ be an $m$-manifold, $N$ be an $n$-manifold, and $O$ be a $p$-manifold. Let $$F: M \rightarrow N\text{ and }G: N \rightarrow O $$ be $C^1$ maps. We want to prove the chain rule for the composition:

Pushforward Map
If $M$ and $N$ are manifolds, then the differential of $F$ is also called the pushforward map, $$ F_*: T_xM \rightarrow T_{F(x)}N, $$ which defined as follows: For any $v \in T_xM$, $$ F_*v = (F\circ c)'(0), $$ where $c: I \rightarrow M$ is a $C^1$ curve such that $c(0)=x$ and $c'(0)=v$. In other words, if $v \in T_xM$ is the velocity vector of a parameterized curve $c$ passing through $x \in M$, then $F_*v \in T_{F(x)}N$ is the velocity vector of the curve $F\circ c: I \rightarrow N$ at $F(x)$.
Chain Rule
Given $x \in M$, we want to find the formula for the pushforward map $$ (G\circ F)_*: T_xM \rightarrow T_{(G\circ F)(x)}O. $$
Given $x \in M$ and $v \in T_xM$, let $c: I \rightarrow M$ be a curve such that $c(0) = x$ and $c'(0) = v$. This in turn defines a curve $$ F\circ c: I \rightarrow N, $$ which satisfies $(F\circ c)(0) = F(x)$ and, by the definition of the pushforward map \begin{align*} (F\circ c)'(0) &= F_*v \end{align*} Therefore, \begin{align*} (G\circ F)_*v &= \left.\frac{d}{dt}\right|_{t=0}(G\circ F)(c(t))\\ &= \left.\frac{d}{dt}\right|_{t=0}G((F\circ c)(t))\\ &= G_*(F\circ c)'(0)\\ &=G_*F_*v\\ &= (G_*\circ F_*)v \end{align*} This proves the chain rule $$ (G\circ F)_* = G_*\circ F_*, $$ as depicted here:
